There’s a paper out today (just published online) by J. C. Fyfe, N. P. Gillett, and F. W. Zwiers, called “Overestimated global warming over the past 20 years”. I’ve addressed this “pause in warming question” at this blog earlier, and the argument they make, based upon the Supplement to the article (which is not behind a payment), is predominantly statistical. The authors are well-known in IPCC circles and, statistically speaking, Zwiers is a co-author with von Storch with the good but somewhat dated book Statistical Analysis in Climate Research (which I own).
But, Judith Curry has commented on the article, and I’m sure it’s going to be a major feature of discussion with the latest IPCC report due out soon. (Added 16th September 2013: In case the reader is not familiar with Judith Curry, this is an example of what’s wrong with Curry’s kind of analysis.)
So, I’m buying a copy of the article, and will do an analysis, reporting here. What’s odd about the material in the Supplement, and I hope they address in the article, is the difference in methodology in apparently what Fyfe, Gillett, and Zwiers did, and what’s been done earlier, which hopefully they’ll contain in their references. I’m thinking specifically of:
- S.-K. Min, D. Simonis, A. Hense, “Probabilistic climate change predictions applying Bayesian model averaging”, Philosophical Transactions of the Royal Society A, 15 August 2007, 365.
- R. L. Smith, C. Tebaldi, D. Nychka, L. O. Mearns, “Bayesian modeling of uncertainty in ensembles of climate models”, Journal of the American Statistical Association, 104(485), March 2009.
I also think it odd that they claim they made no distributional assumptions in the derivation in their Supplement, which I find highly dubious. I mean, there are no explicit distribution assumptions made when you do linear least squares, but it’s provable that it is equivalent to a Gaussian model of errors.
Later.
Postscript: 30th August 2013, 12:56 EDT.
I am delving deeply into the techniques of this interesting meta-analysis, with kind help of Professor Francis Zwiers. Of course, anything I say or present here is my own technical responsibility, not his. I will probably write a white paper on this, sharing it with Professor Zwiers, and presenting highlights here.
Postscript: 31st August 2013, 09:52 EDT.
Jokimäki posts “Global warming … Still happening” at the SkepticalScience blog and indeed it is. Has to be, lest basic, 19th century-derived physics be violated, not to mention our engineering of spacecraft and semiconductors. It will be very interesting rationalizing the Rahmstorf (with Foster and Cazenave) kinds of projections he reports with this Fyfe, Gillett, and Zwiers paper. And a good chance to contribute to improving the statistical arsenal applicable to climate work. Right now I’m having a serious look at empirical likelihood techniques, as used in nested sampling and approximate Bayesian computation. (See, for instance, Professor Christian Robert’s talk, or Lazar, “Bayesian empirical likelihood”, Biometrika, 2003.)






Jan
thanks so much. This is a great explanation. I think this article puts to lie the idea that the models are highly inaccurate. Zeke Hausfather, Henri F. Drake, Tristan Abbott, Gavin A. Schmidt, Evaluating the performance of past climate model projections, GRL, AGU100, December, 2019, https://doi.org/10.1029/2019GL085378.
Another thought occurred to me. Since ocean are absorbing more than 90% of the heat imbalance, if the ocean/atmosphere model underestimates the heat absorbed by the ocean by only 1% then the amount of heat left to warm the surface will be overestimated by 10%. But that extra heat in the ocean will increase sea level, melt ice sheets and decompose methane clathrate and eventually will come back to haunt us later since the imbalance still exists.
Anyway, I have always agrees with Tamino that the evidence of a hiatus was scant.
best
Tony
@Tony Noerpel,
Actually, yes, although they were not peer reviewed. See:
In the original article at Nature Climate Change, open access for a time because of broad interest, there was a list of blog articles commenting on it shown, including the two above. Unfortunately, that door is now closed, and it is behind a paywall. I do not have a subscription, nor do I have access through my alumni privileges at MIT.
Fyfe himself has disagreed with my assessment, although he did not cite me by reference or name. That’s good because it suggests others saw a similar thing. The discrepancy has to my mind never been satisfactorily established, there’s never been an admission of blemish from the original authors, despite what appears, in the field, to be the after-the-fact-based-upon-more-data revision that the determination of hiatus was premature. The most direct comment came in critiques by Lewandowsky, et al (2015), by Tamino (2019), and by Risbey, et al (2018) (with a comment from Tamino who, by the way, was a co-author). The Lewandowsky, et al paper was as much a delve into the sociology of natural science as a comment on geophysical fact.
There was even a rebuttal article with authored by a famous group of climate scientists including two of the original three authors:
“Making sense of the early-2000s warming slowdown“, Nature Climate Change, 6, 224-228 (2016). Their point was to deflect the criticism of Lewandowsky, et al, which they appeared to be particularly piqued by (but read it yourself!). My interest, necessarily, was the following excerpt of that paper:
The cited references are:
[1] Flato, et al. Evaluation of Climate Models. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T.F., D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P.M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
[4] T. R. Karl, et al, “Possible artifacts of data biases in the recent global surface warming hiatus”, Science 26 Jun 2015:
348(6242), 1469-1472 [DOI: 10.1126/science.aaa5632]
[9] Rajaratnam, B., Romano, J., Tsiang, M. et al., “”Debunking the climate hiatus“, Climatic Change, 2015, 133, 129-140 (open access)
What’s most interesting to me is that the Fyfe, Meehl, et al (2016) parry of criticism of a warming slowdown does not address the original observations of Fyfe, Gillett, and Zwiers (2013). FGZ chose 1993-2012 and 1998-2012 as their periods of study. Fyfe, Meehl, et al (2016) in their Figure 1 go all the way back to 1950 and subdivide the interval into 5 subintervals, each of which demonstrates both different variability and certainly non-stationarity in statistics. Also, the last two subintervals, roughly corresponding to the FGZ comment of interest, shows a broadly wider envelope of uncertainty. This has two implications.
First, if there is anything like non-stationarity in subintervals, then the comparison of FGZ’s Figure 1 is surely invalid, because it is posing the problem as if it were a two sample t-test. That assumes a bunch of things, including independence of observations. They even went on to calculate a darn p-value from this and made what I consider to be statistically outrageous claims based upon it.
Second, the wider an envelope of uncertainty for a trend, the less confidence there is that the mean trendline or the 0.50 quantile trendline lie where they are estimated to lie. Accordingly, that slope in the region of question could be anything: Up, down, or in-between. This is primarily what Tamino and Ripley, et al () argue, and they are entirely correct.
I’m amused by what surely is an artificial distinction by Fyfe, Meehl, et al between what they deem as “the purely statistical aspects of the slowdown” and “improving process understanding and assessing whether the observed trends are consistent with our expectations based on climate models”. Um, the latter is what Statistics as a field does. Surely, Statistics is not going to tell the entire story, but it is the beginning. Moreover, if a story grossly violates statistical principles, it necessarily has problems.
So, while Lewandowsky, et al (2015) may not have been an entirely statistical or physical science criticism of the claims of a warming slowdown, they were on to something, that there is/was, in my opinion, some kind of circling of wagons here, to climate science’s detriment.
Jan did you ever publish a commentary on this Fyfe paper? I’d be interested in reading it.
Pingback: Less evidence for a global warming hiatus | Hypergeometric
My understanding of Fyfe, Gillett, and Zwiers 2013 (“FGZ” hereafter) is that on one side there’s HadCRUT4 and its ensembles, and on the other side there are the models from CMIP5, run against presumably representative forcings from measurements of the years in question, and then results then compared against the HadCRUT4 ensembles. The basic thing is that HadCRUT4 comes in low, and the smear of the CMIP5 models comes in on median higher, even if there is overlap. They then declare that the models are exaggerating warming and use a p-value to assess how badly.
Without getting too long or technical — happy to share my write-up after I share it with Zwiers, which I promised I would do — there are three possibilities ….
(1) Maybe the HadCRUT4 realizes a particular Earth climate future which is one of a possible many. After all, we only see one path from an initialization, even if many were stochastically possible.
(2) Maybe the initial and boundary conditions of the models did not precisely capture the same conditions that HadCRUT4 implies or induces and, so, even if the models were physically correct, they were not simulating the same Earth climate.
(3) Maybe there is something fundamentally off about the assumption of exchangeability, by which I assume they mean de Finetti exchangeability, which invalidates the comparison they want to do.
I am, of course, intrigued by this last possibility, although I don’t know how I would construct an assessment of whether the exchangeability assumption was warranted or not. It’s not like we can construct the joints directly. Maybe there’s some chain of conditionals by which we can get there?
At least, my consensus is that I think the conclusion in the title is extreme considering the evidence of the paper, which is basically just a curious study, perhaps worthy of the “Comment” status the journal affords it, but people, like Dr Judith Curry, apparently declared it to be much more.
There is something profoundly unsatisfying about the Chinese menu approach to statistical analysis which von Stoch and Zwiers appear to embrace in their STATISTICAL ANALYSIS IN CLIMATE RESEARCH, as it offers a bunch of techniques with only technical authority and citation density as being their justification. I’d rather have a more uniformly calculated set of methods which could be compared with greater ease, and I feel the Bayesian mindset just gives us that.
As in medicine, a lot, but far from all, of the geophysical community is still back in Frequentist Land.
Regarding your comment on NS, to the degree the narrow algorithm has those limitations, yeah. But it seems to me its insight is that level sets of likelihoods (or sampling densities) explored by supports implied by priors is a good way to look at things, however way each of those pieces gets realized.
This is exactly why I enjoy your blog: to discover these statistically interesting climate change papers and to get some insight into why they do things they way they do them! The common ancestries of climate change models must indeed introduce some difficulties into the interpretation of their ensemble predictions via frequentist style tests. This Eint_ij, Mij notation and explanations from the supplementary data look quite like the structural equation modelling used in some survey-based meta analyses. But one very basic question which I couldn’t glean from the paper itself is: are these “predictions” the output of models run with only data available up to the starting year, or do they update their models from partial data throughout the duration of the simulation?
Re: nested sampling. There is indeed a lot of good work on this from the astronomical (& physics) community; particularly with the production of publically-available codes for running quick NS analyses. NS hasn’t been widely embraced by the general statistics community though: one reason might be that it only works efficiently (via ellipse-based sampling) on R^n space problems with separable priors, and another reason might be that it’s not amenable to Gibbs sampling techniques.
Dr Cameron, honored to have your opinion here. As an aside, I am learning and admiring the work the astro community has done with Bayesian inference, notably embracing the Nested Sampling work of Skilling and his disciplines (Feroz, Hobson, Bridges, and others), which I greatly admire.
As to Fyfe, Gillett, Zwiers, as noted, I am working a critical review where I think I know what’s going on, but am going back to original papers on HadCRUT4 and summary papers describing the 37 models from CMIP5 they used to try to understand what’s going on. That, and other commitments, have delayed the project.
I am drilling down into what “exchangeability” means precisely in this context, trying to connect it to de Finetti’s Theorem. But, I think, more importantly, even if the HadCRUT4 observations represent ensembles, they capture essentially one run of Earth for the period in question. So, thinking Rubin and Aitkin Bayesian bootstrap, I wonder if there aren’t other ensembles which were very possible and so should be represented in some kind of prior, but aren’t manifest. I see the primary sin of the frequentist bootstrap limiting values to only those observed, where there are actually those values and whole neighborhoods of them which are admissible.
I also worry about interdependency …. Climate models have ancestries and common components. Fyfe, Gillett, and Zwiers chose to use them as if they were black boxes but I bet that if denotes the HadCRUT4 ensemble data and
denotes the HadCRUT4 ensemble data and  the
the  -th model,
-th model, 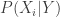 is dependent upon one or more
is dependent upon one or more  and to pretend otherwise makes things seem more inconsistent than they are.
and to pretend otherwise makes things seem more inconsistent than they are.
Finally, there are a slew of small things, such as how trends are ascertained and what precisely is meant by “internal variability”. They say (in their supplement) “ and
and 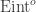 are perturbations to
are perturbations to  and
and  respectively due to internal variability. These are different for each model run, but are essentially identical for each resample of the observations.” That last bit seems quite incomplete. I don’t know how they would fix it, but, then, maybe the idea of comparing this set of observations and the model runs is just a broken one.
respectively due to internal variability. These are different for each model run, but are essentially identical for each resample of the observations.” That last bit seems quite incomplete. I don’t know how they would fix it, but, then, maybe the idea of comparing this set of observations and the model runs is just a broken one.
All these somewhat deep issues and trying to describe them in understandable and compelling language.
One observation from a climate change science neophyte: 117 draws from the model distribution seems insufficient to accurately estimate a 95% CI (or an empirical reference distribution) for hypothesis testing. Presumably the 117 comes from limitations of computational power/time, but I would imagine that an importance sampling type strategy could have been used to choose from uncertain inputs targeting the tails of the model reference distribution. As a trivial example, 117 draws from the standard normal gives an empirical 2.5% quantile with repeat simulation (from 1000 repeats) mean of -1.88 with standard deviation of 0.22. Importance sampling 117 draws from a Student’s t gives a repeat simulation mean of -1.98 with standard deviation of 0.17. The truth being -1.96, of course!
Pingback: “p-values are random variables” | Hypergeometric